Data Structure V Tree III

Posted on | Edited on | In | | Views:

─=≡Σ((( つ•̀ω•́)つ BS🌲

Article Language: English
Example Language: Java
Reading Time: 6min

We often use recursion to solve the problem that involves tree(data structure). A binary tree has three parts, left subtree, root, and right subtree. This logic applies to every node in the tree including leaf nodes. If it has back track, it would be easier to just use recursion. However, if it is a tail trcursion, it can be converted into simple loops.

Under this broad definition, however, every algorithm that uses recursion or loops could be regarded as a “divide and conquer algorithm”[1].

Search in Binary Search Tree

input: A root of a tree, and a target value.
output: If exist, return the node; otherwise, return null.

In a binary search tree, every node must satisfy the property that values in the left subtree must not be greater than it, and the value in the right subtree must not smaller than it. So we can recursively call the function. If the node value is smaller than target, look to its right. Otherwise, look to the left. Every time the function being called, the searching range is reduced to half. For a tree that has n nodes. The time complexity is O(logn). The space complexity is O(height) as well. However, the worst case could be O(n) if the tree is linear.

Recursion

1
2
3
4
5
6
7
8
9
10
11
12
public TreeNode searchBST(TreeNode root, int target) {
	if (root == null) return null;

	if (root.val < target) {
		return searchBST(root.right, target);
	}
	if(root.val > target) {
		return searchBST(root.left, target);
	}

	return root.val == target ? root : null;
}

Iteration
Time comlexity is the same. However, the space is O(1) in iteration.

1
2
3
4
5
6
7
8
9
10
11
12
public TreeNode searchBST(TreeNode root, int target) {
	if (root == null) return null;

	while (root != null && root.val != target) {
		if (root.val < target) {
			root = root.right;
		} else {
			root = root.left;
		}
	}
	return root;
}

如果所有的问题都这么简单, 世界该多么美好 ✧୧(๑=̴̀⌄=̴́๑)૭✧ ꒰

Insert in Binary Search Tree

input: A root and a target.
output: Return the root after insertion (maintain its BST property). If the target exists in the tree, do nothing.

There would be two steps:

  1. find the position for the node. Since it’s a binary search tree with no duplicate values, we can possibility find the postion under a leaf node.
  2. connect the node to the tree.

Time compexity would be O(logn), where n is the number of node in the tree.
Space compexity is the call stack, which is O(height).

Recursion

1
2
3
4
5
6
7
8
9
10
11
12
public TreeNode insert(TreeNode root, int target) {
	if (root == null) return new TreeNode(target);

	if (root.val < target) {
		root.right = insert(root.right, target);
	}
	if (root.val > target) {
		root.left = insert(root.left, target);
	}

	return root;
}

Iteration
Time complexity is O(logn).
Space complexity is O(1).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public TreeNode insert(TreeNode root, int target) {
	if (root == null) return new TreeNode(target);

	TreeNode cur = root;
	TreeNode insetNode = new TreeNode(target);
	while (cur != null && cur.val != target) {
		if (cur.val > target) {
			if (cur.left == null) {
				cur.left = insertNode;
				break;
			} else {
				cur = cur.left;
			}
		} else {
			if (cur.right == null) {
				cur.right = insertNode;
				break;
			} else {
				cur = cur.right;
			}
		}
	}
	return root;
}

Detele in Binary Search Tree

input: A root and the target.
outpit: Return the root after deleting the target node in the tree (must maintain its BST property). If target doesn’t exist, simply return the root.

There will be two steps:

  1. Find the node. Simply search in the tree.
  2. Adjust the structure after deletion.
    • There will be 4 cases when deleting a node:
    1. The node is leaf node –> simply delete
    2. The node only has left/right subtree –> percolate up left/right subtree’s root. Since the subtree itself is a BST , it’s a subtree of the target node and it has no siblings (no need to compare with left/right subtree), it will maintain the property after lifting up.
    3. The node has both left and right subtree –> pick a side, taking the largest node that is smaller than the node (look the left) or the smallest node that is greater than the node (look the right).
      • Since we’re looking for the largest smaller one or the smallest larger one, there will be two situations that need to be considered.
      1. If the left subtree of the target doesn’t have a right subtree or the right subtree of the target doesn’t have a left subtree. Then the root of the subtree is the candidate. Due to the property of bst, all the left subtree is smaller than it and all the right subtree is greater than it for every node in the tree.
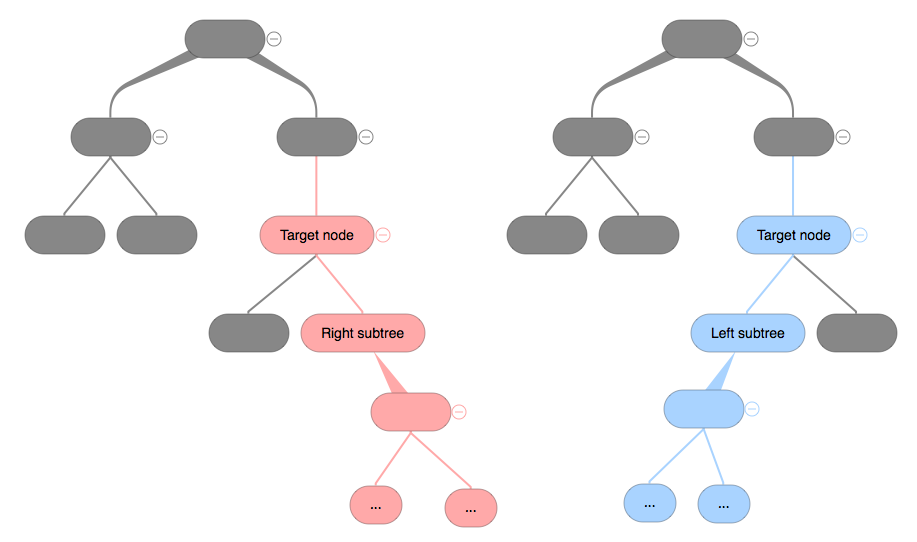
      2. If the left/right subtree of the target node has both left and right children, implement a helper function to find the left/right most node.

For a tree with n nodes, time complexity for searching target takes O(logn), and adjustment can take O(height) for getting the left/right most node in the subtree. Therefore, the time complexity is O(2 * height), then is O(height). Space complexity is O(height) for stack frame if using recursion.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
public TreeNode delete(TreeNode root, in target) {
	if (root == null) return null;

	//Step1. find the node
	if (root.val > target) {
		root.left = delete(root.left, target);
		return root;
	} else if (root.val < target) {
		root.right = delete(root.right, target);
		return root;
	}

	//Step2. current root is target, adjustment
	//root != null && root.val == target;
	//case11 & 2
	if (root.left == null) {
		return root.right;
	} else if (root.right == null) {
		return root.left;
	}
	//root.left != null && root.right != null
	//case3.1 pick right
	if (root.right.left == null) {
		root.right.left = root.left;
		return root.right;
	}
	//case3.2 pick right, then find the smallest in the right subtree;
	TreeNode smallest = findSmallest(root.right);

	//reconnect the node, then return.
	smallest.left = root.left;
	smallest.right = root.right;
	return smallest;
}

private TreeNode findSmallest(TreeNode node) {
	TreeNode prev = node;
	node = node.left;
	while (node.left != null) {
		prev = node;
		node = node.left;
	}
	//node.left == null, current node is the left most. pre is current at the parent of node.
	pre.left = node.right;
	return node;
	}
}

[1]: “Divide and Conquer Algorithm.” Wikipedia, Wikimedia Foundation, 3 Apr. 2018, en.wikipedia.org/wiki/Divide_and_conquer_algorithm.